Desarrollo de una clase de Matemática mediante la Resolución de Problemas

Análisis y posible solución del problema

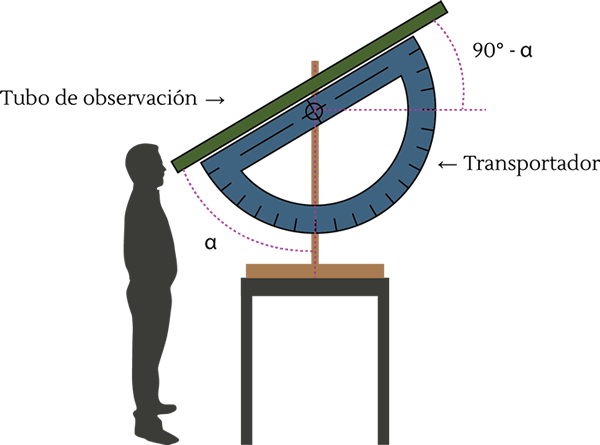
Se espera que las y los estudiantes representen el problema mediante un dibujo similar a este:

Mediante el trabajo individual o grupal el estudiantado puede proponer alguna de las siguientes soluciones:

1. Empleando cinta métrica, regla, cuerdas y transportador, puede recrearse la situación. Realizar una proyección hacia una pared de los 2,6 m (desde el piso o desde la altura de una mesa) y con ayuda del transportador y una regla retroceder hasta poder observar los 2,6 m usando una amplitud de 15º. De esta forma, se puede determinar una aproximación de la distancia buscada (noción intuitiva del teodolito).

Se espera que las respuestas se aproximen a los 9,70 m.

2. El estudiantado conoce el Teorema de Pitágoras e intentará determinar la medida de los lados del triángulo; especulará las otras dos medidas, pero garantizará el ángulo de 90º. Para tal fin utilizará la calculadora y calculará lo siguiente:

Intento 1: Triángulo isósceles rectángulo, ángulos de 90º, 45º y 45º
Cateto	Cateto	Hipotenusa
2,6	2,6	3,67
Intento 2: Triángulo cuyo cateto menor es duplicado por la medida del otro cateto y se desconoce exactamente la medida de los ángulos. Pero pueden asumir erróneamente que los ángulos mantienen esa proporción; o sea, que uno mide 22,5º y el otro 67,5º.
Cateto	Cateto	Hipotenusa
2,6	5,2	5,81
Intento 3: Triángulo cuyo cateto menor es triplicado por la medida del otro cateto y se desconoce exactamente la medida de los ángulos. Pero pueden asumir erróneamente que los ángulos mantienen esa proporción; o sea que uno mide 15º y el otro 75º.
Cateto	Cateto	Hipotenusa
2,6	7,8	8,22

Despúes de este trabajo las y los estudiantes pueden responder que la distancia era de 7,8 m.

Recordemos que según la metodología de resolución de problemas, el estudiantado debe resolver el problema con sus conocimientos previos. Por lo tanto, se mostraron dos posibles formas que se pueden emplearse para resolver el problema; sin embargo, pueden haber otras no incluidas aquí.

Cuando la mayoría de las y los estudiantes hayan podido encontrar alguna solución, debe realizarse una plenaria en la que se expongan las soluciones (de algunos y algunas estudiantes o de cada subgrupo). En este momento, el o la docente debe estar muy atento a los aportes de las y los estudiantes, así como de las respuestas que se brinden. Puede ser apropiado tomar nota, ya que las ideas de las y los estudiantes deben ser utilizados para el cierre o la clausura de la clase.

Analice la  respuesta al problema empleando Trigonometría para posteriormente ejemplarizar el proceso de cierre o clausura:

Se representará la distancia entre el gimnasio y el inicio de la rampa con la letra $y$; entonces, empleando la función trigonométrica tangente, se puede encontra el dato de interés de la siguiente forma:
$ tan \, 15^{\circ} = \frac {2,6} {y} $, despejando  se obtiene que:
$ y = \frac{2,6} {tan \, 15^{\circ}} $
$ y = 9,70m $

Cuando el docente inicia el cierre o la clausura, deben converger el trabajo estudiantil independiente, la discusión interactiva de la solución y el trabajo de cierre que es responsabilidad del docente.

Se puede comenzar indicando que existen otras herramientas matemáticas que pueden facilitar el trabajo realizado para encontrar la respuesta al problema. Esas herramientas son las razones trigonométricas y que establecen relaciones entre las medidas de los lados del triángulo y sus ángulos.
Puede emplear en este momento la experiencia de las y los estudiantes que recrearon la situación, apuntado la importancia de conocer el ángulo, establecer la altura, las herramientas que usaron y cómo lograron encontrar una medida aproximada. Se espera que ellos y ellas narren como tuvieron que retroceder o acercase a la pared hasta lograr que la amplitud del ángulo, al moverlo hacia arriba y abajo abarcara los 2,6 m, y luego midieron la distancia entre la posición donde se colocó el transportador y la pared. Asimismo, en la experiencia narrada por el estudiantado se espera que utilicen palabras como opuesto, de frente al ángulo, cateto, ángulo de elevación, mirar hacia arriba. Dicho tipo de vocabulario debe ser retomado por el docente y empleado para formalizar el conocimiento.

Respecto de la segunda solución presentada, el o la docente puede retomar elementos muy valiosos y generar una discusión acerca de la veracidad y pertinencia de la suposición del comportamiento de los ángulos en relación con los lados del triángulo.

Y emplear una comparación de la respuesta encontrada con la respuesta real para determinar que es incorrecta la suposición a propósito de la relación entre la medida de los lados y los ángulos del triángulo.

Finalmente, el docente debe mostrar la solución del problema mediante Trigonometría y comprobar la razón de la tangente mediante la verificación de ambos lados de la igualdad, el cociente entre los catetos $\frac {2,6}{9,70}$ y la $ tan \, 15^{\circ} $. También, debe aprovechar el problema para formalizar las otras dos razones trigonométricas restantes, así como los ángulos de elevación y depresión. En el punto 5 del apartado Presentación de una clase mediante la resolución de un problemas, se ofrecen los conocimientos a formalizar de manera detallada.

 

 

Anterior

Siguiente

Arriba