Desarrollo de una clase de Matemática mediante la Resolución de Problemas

Presentación de una clase mediante la Resolución de Problemas

Según los programas de Matemáticas del MEP (2012), uno de los temas por tratar es la Trigonometría, que se encuentra en el área de Geometría. Para efectos del problema que se va ha plantear, se trabajaran los siguientes conocimeintos directamente: tangente, ángulos de elevación y depresión. Y las siguientes habilidades específicas:

• Aplicar las razones trigonométricas básicas (seno, coseno y tangente) en diversos contextos
• Aplicar los conceptos de ángulos de elevación y depresión en diferentes contextos
• Resolver problemas que involucren la razones trigonométricas, sus propiedades y ángulos de elevación y depresión.

Es importante indicar que el estudiantado ya debe conocer el Teorema de Pitágoras.

Iniciando la clase

1. El o la docente puede iniciar la clase con una breve reflexión sobre la Ley 7 600, para sensibilizar a los estudiantes sobre la importancia de respetar las demarcaciones de espacio en autobuses y parqueos entre otros. Así como el derecho de todas las personas a tener las mismas oportunidades de acceso.

2.  Posteriormente se les presenta al estudiantado el siguiente problema:

3. Se puede indicar al estudiantado la estrategia de trabajo por seguir:

1. Se trabaja individualmente el problema.
2. Se trabaja en forma grupal el problema.

Para cualquiera de las opciones elegidas, debe brindarse al estudiantado el tiempo suficiente con el fin de resolver el problema; en el siguiente apartado se presentará una posible solución al problema y se evidenciará la necesidad del tiempo para realizar dibujos, establecer estrategias de solución, llevar a cabo procedimientos erróneos y proponer una respuesta al problema.

4. Seguidamente, después de que los y las estudiantes hayan trabajado con el problema, se deben compartir los resultados o las respuestas halladas,  así como las estrategias de trabajo utilizadas. Puede realizarse mediante una sesión plenaria en la que se exponen las ideas con las que lograron dar respuesta al problema. Es de suma importancia que el docente esté atento al aporte de los y las estudiantes, que tome nota de sus comentarios, estrategias, respuestas, argumentos y soluciones porque debe emplear tales recursos al cerrar el tema.

5. El final de la sesión (el trabajo de los y las estudiantes y la plenaria) puede requerir hasta 3 o 4 lecciones; en este momento el o la docente debe formalizar el conocimiento que se pretendía adquirir. Lo anterior, según la Escuela Francesa, en la Teoría de las Situaciones Didácticas de Brousseau (similar a la institucionalización del saber)  para el MEP es denominado el cierre o la clausura.

En este momento el o la docente debe tratar de establecer una relación entre el trabajo cognitivo y las respuestas halladas por los y las estudiantes y el conocimiento por formalizar, el cual está presente desde el diseño del problema; además, pueden formalizarse otros conceptos que estén relacionados con la temática. Una forma de hacerlo es la siguiente:

Ángulos de elevación y depresión

Cuando se observa algún objeto, existen dos posiciones en las que se realiza la observación: mirando hacia arriba (en el caso de la construcción de la rampa) o mirando hacia abajo; sin embargo, en ambos casos debe haber un punto de referencia que se denomina línea horizontal.

A partir de la línea horizontal, usted puede mirar hacia arriba a lo cual se le denomina ángulo de elevación, que corresponde a la amplitud registrada entre la línea horizontal y la línea visual que se traza hasta el objeto de interés.

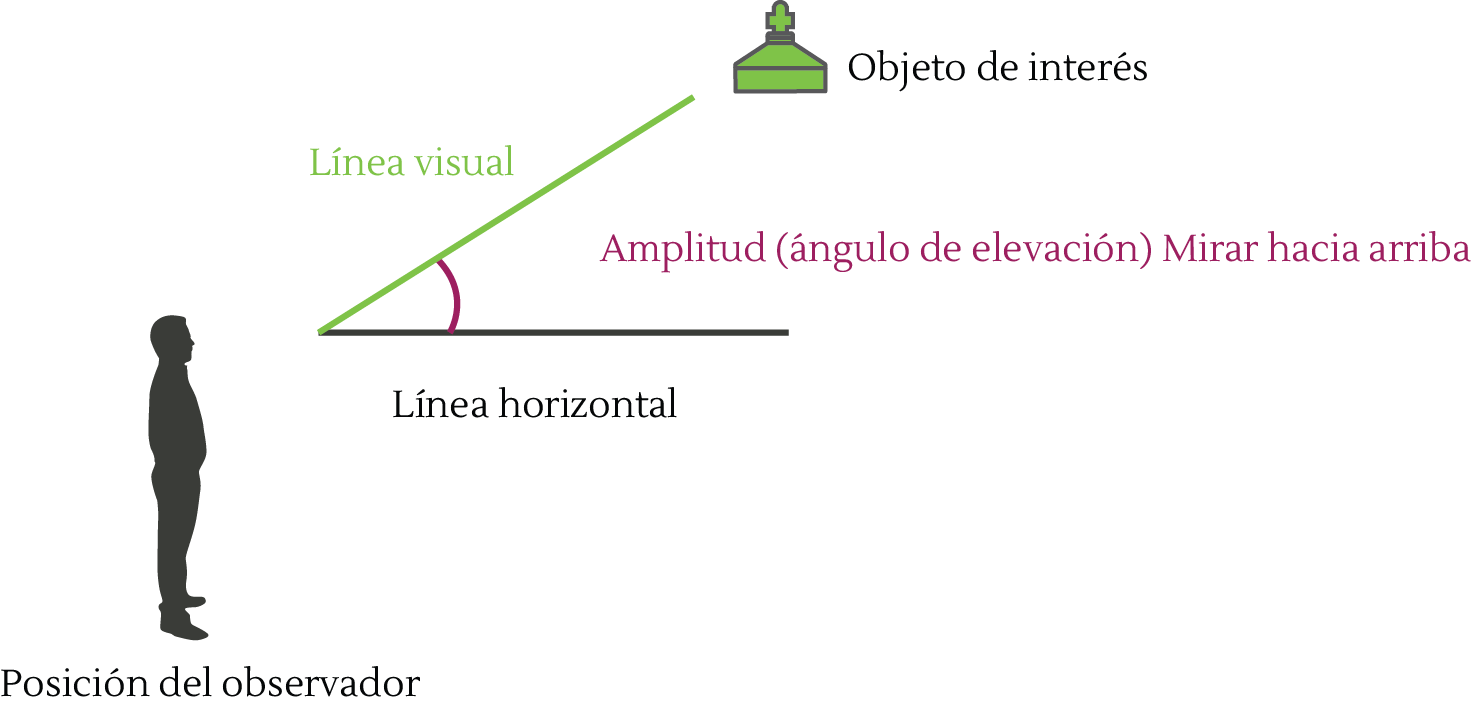
A partir de la línea horizontal, usted puede mirar hacia abajo, a lo cual se le denomina ángulo de depresión, que corresponde a la amplitud registrada entre la línea horizontal y la línea visual trazada hasta el objeto de interés.

 

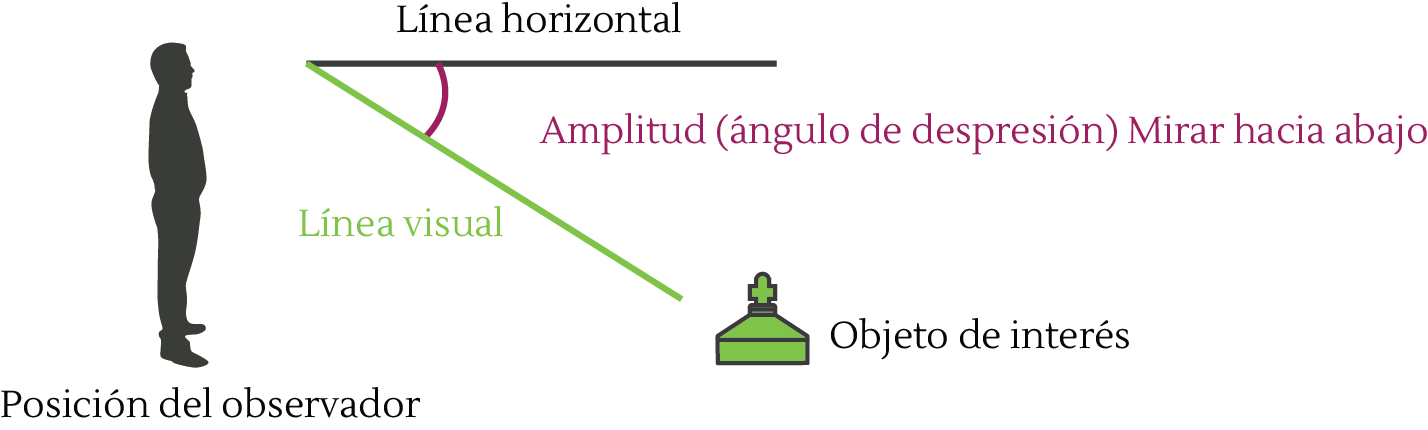
Razones trigonométricas

Las razones trigonométricas corresponden a la relación entre las longitudes de dos lados de un triángulo rectángulo en relación con cada uno de sus ángulos agudos. Las tres razones trigonométricas básicas son el seno, el coseno y la tangente. Estas se abrevian respectivamente como sen, cos y tan.

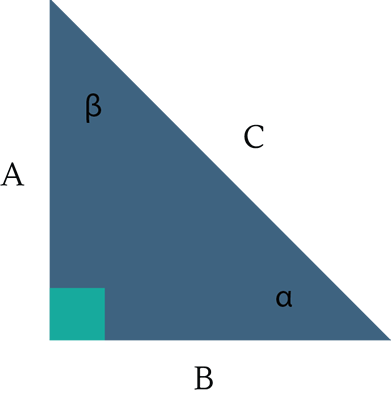
Las razones trigonométricas corresponden a:

$ Sen \, a = \frac{A}{C} $, respecto del ángulo agudo $a$, el lado $A$ corresponde al lado opuesto y $C$ corresponde a la hipotenusa.

$ Cos \, a = \frac{B}{C} $, respecto del ángulo agudo $a$, el lado $B$ corresponde al lado adyacente y $C$ corresponde a la hipotenusa.

$ Tan \, a = \frac{A}{B} $, respecto del ángulo agudo $a$, el lado $A$ corresponde al lado opuesto y $B$ corresponde al lado adyacente.

6. Finalmente, el o la docente puede presentar un extracto de algún documental acerca de historia de la matemática, con el objetivo de mostrar ¿cómo las sociedades antiguas, los indúes en particular, utilizaron sus conocimientos en Geometría para desarrollar la Trigonometría? Además, de algunas de las aplicaciones. Un material como el sugerido puede emplearse para motivar a las y los estudiantes.

 

 

Anterior

Siguiente

Arriba